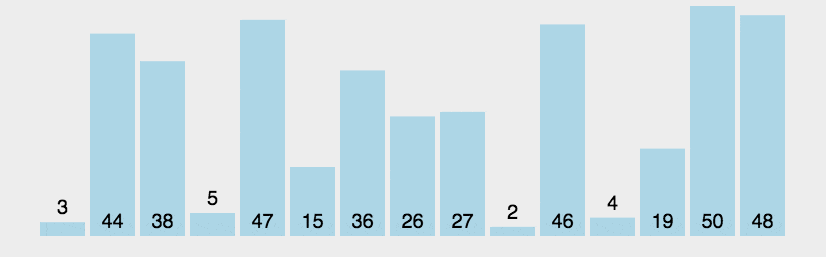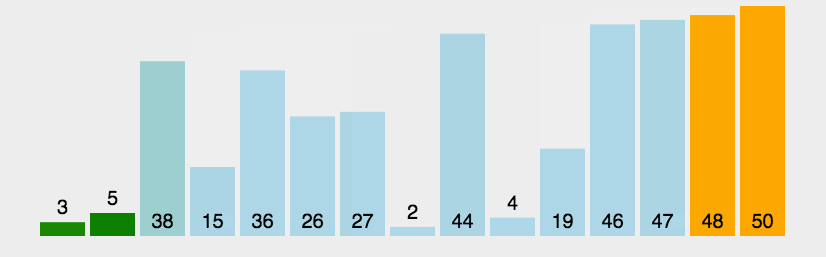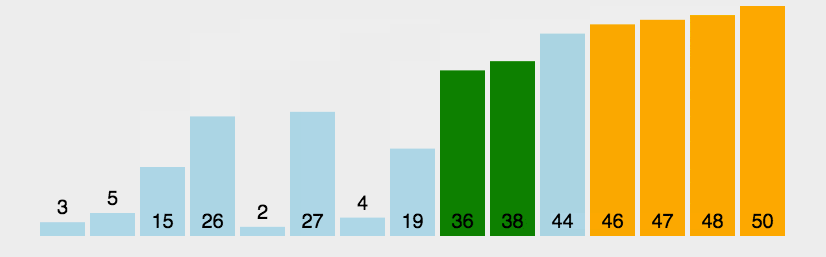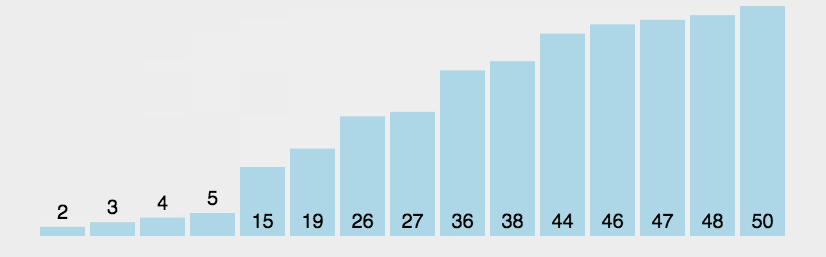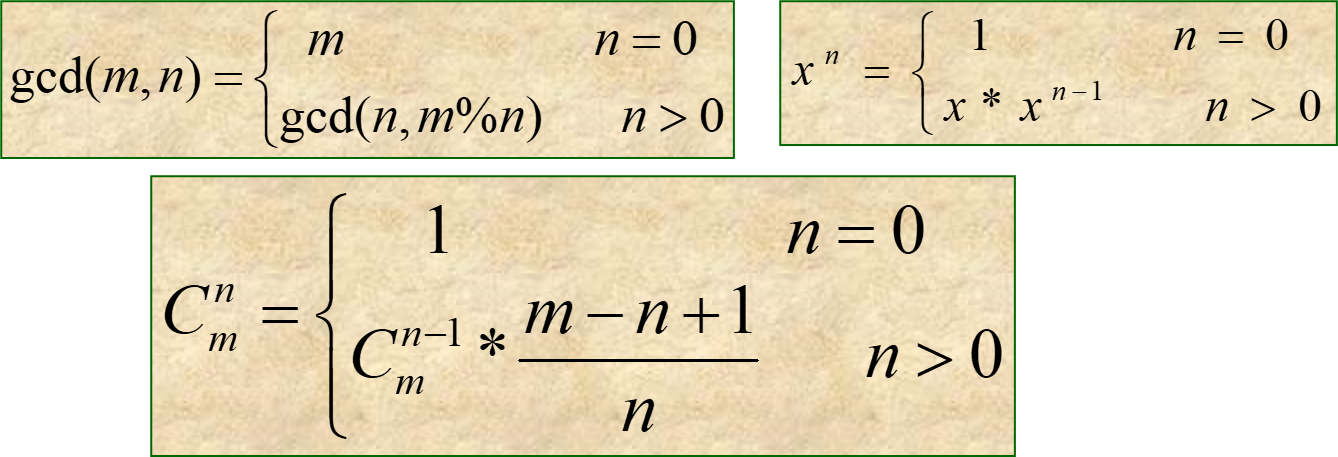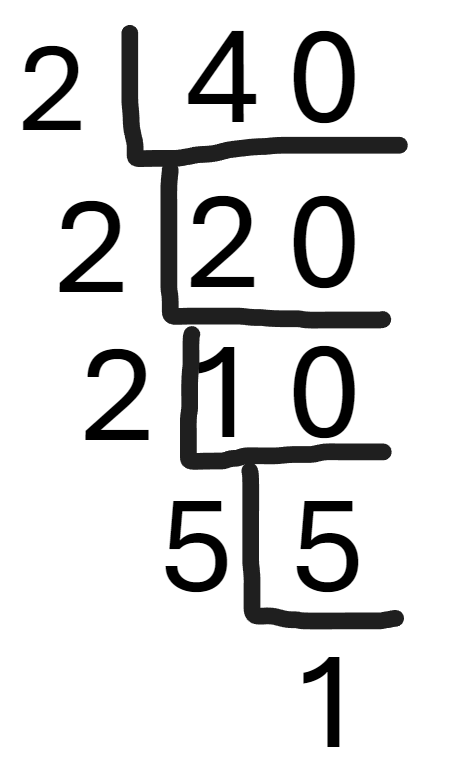整理一下所学知识以及课上ppt的内容!(`・ω・)
算法相关
排序 相关文章
三数排序 一个简单的冒泡排序的变种,通过多次比较和交换来确保三个数按升序排列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void sort () {int a, b, c, t;scanf ("%d%d%d" , &a, &b, &c);if (a > b) {if (b > c) {if (a > b) {printf ("%d %d %d\n" , a, b, c);
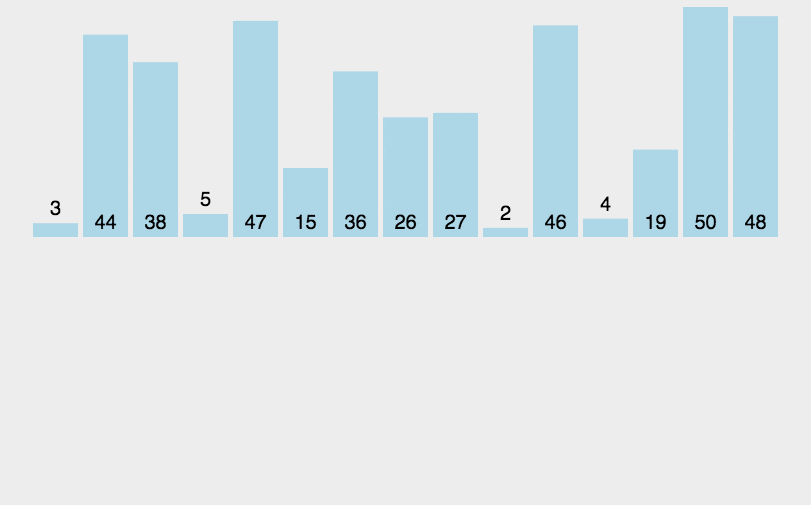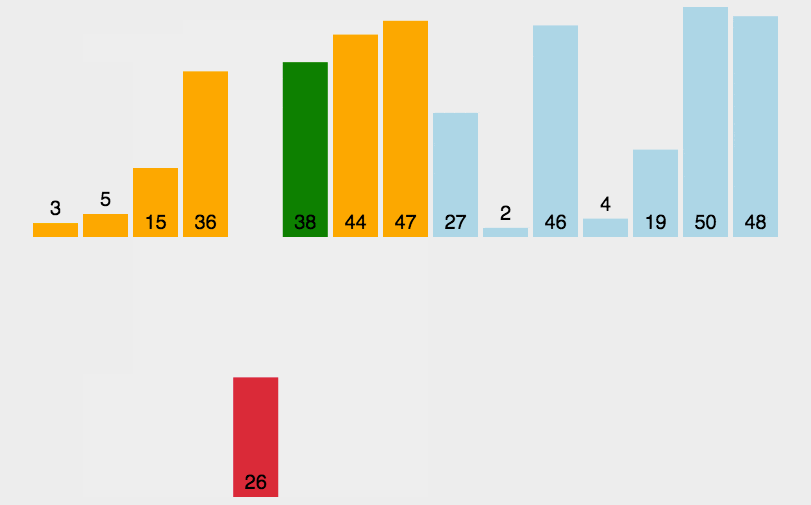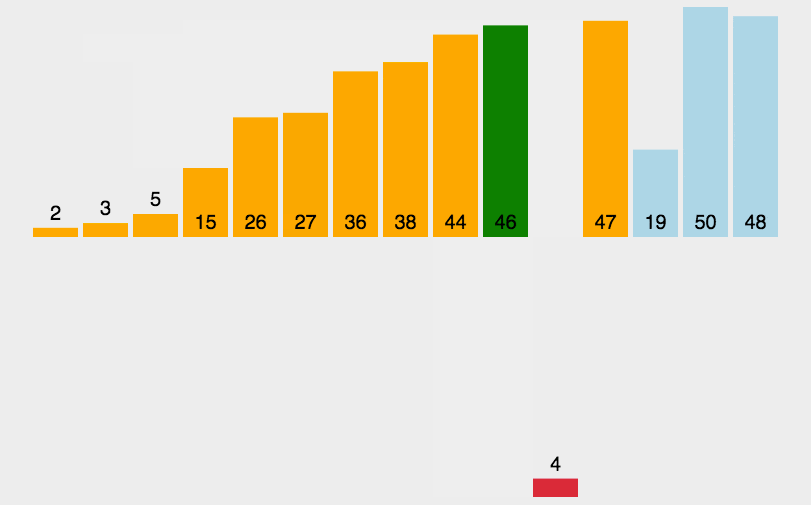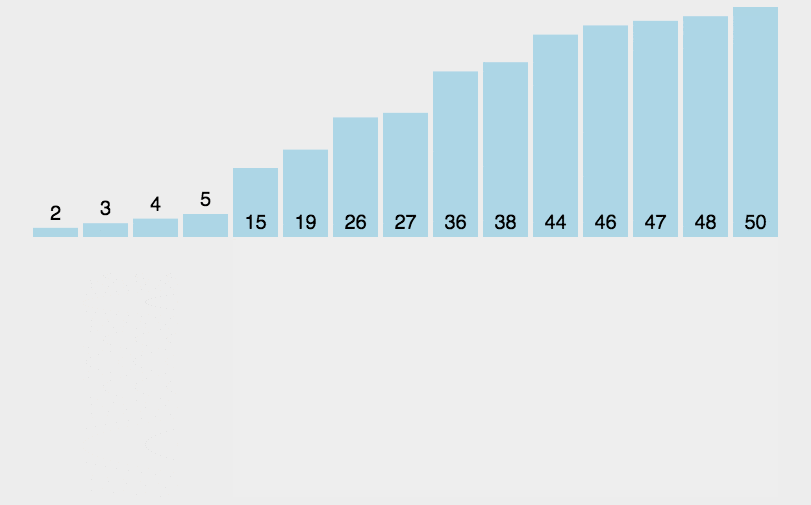
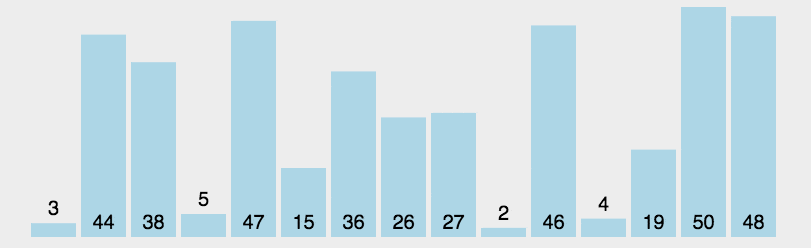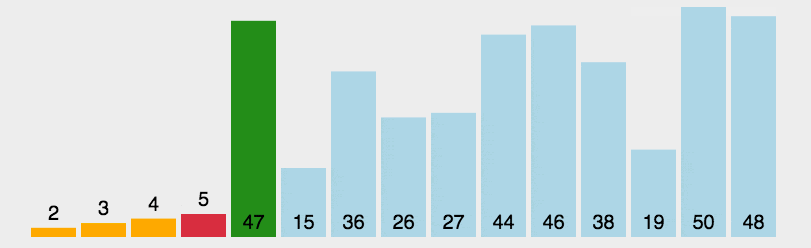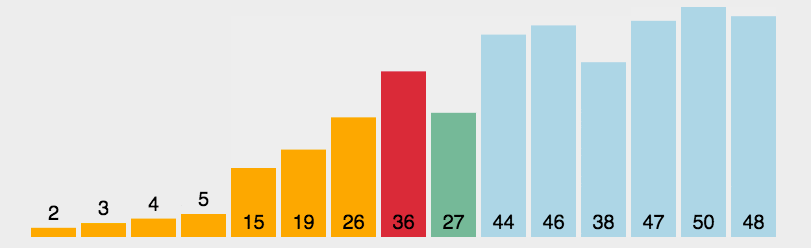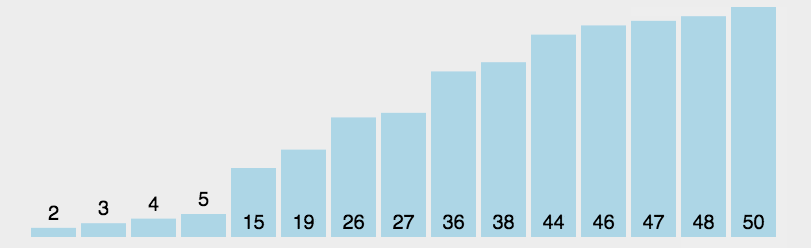
冒泡排序 原地排序,稳定,
O ( n 2 ) O(n^{2}) O ( n 2 )
基本思想:通过相邻数据的交换来达到排序的目的。
排序过程:
比较第一个数与第二个数,若为逆序a[0]>a[1],则交换;然后比较第二个数与第三个数;依次类推,直至第n-1个数和第n个数比较为止——第一趟冒泡排序,结果最大的数被安置在最后一个元素位置上;
对前n-1个数进行第二趟冒泡排序,结果使次大的数被安置在第n-1个元素位置;
重复上述过程,共经过n-1趟冒泡排序后,排序结束
排序总轮数 = 元素个数 - 1
for (i = 0 ; i < N-1 ; i++){for (j = 0 ; j < N-1 -i; j++){if (a[j] > a[j+1 ]){1 ];1 ] = t;
插入排序 原地排序,稳定,
O ( n 2 ) O(n^{2}) O ( n 2 )
基本思想:通过对未排序的数据逐个插入合适的位置而完成排序工作。
排序过程:
首先对数组的前两个数进行从小到大的排序——第一趟插入排序;
接着将第3个数与排好序的两个数比较,将第3个数插入到合适的位置——第二趟插入排序;
重复上述过程,直到把最后一个数据插入合适的位置,共经过n-1趟排序后,排序结束。
for (i = 1 ; i < N; i++){for (j = i-1 ; j >= 0 && t < a[j]; --j){1 ]=a[j];if (j != i-1 ) 1 ] = t;
选择排序 原地排序,不稳定 ,
O ( n 2 ) O(n^{2}) O ( n 2 )
基本思想:在每一步中选取最小值来重新排列,从而达到排序的目的。
排序过程:
首先通过n-1次比较,从n个数中找出最小的, 将它与第一个数交换——第一趟选择排序,结果最小的数被安置在第一个元素位置上;
再通过n-2次比较,从剩余的n-1个数中找出关键字次小的记录,将它与第二个数交换——第二趟选择排序;
重复上述过程,共经过n-1趟排序后,排序结束。
for (i = 0 ; i < N-1 ; i++){ for (j = i+1 ; j < N; j++)if (a[k]>a[j]) if (k != i){
二分
定义:按折半的方法在一个有序数组 中查找一个给定值的元素。
过程:每次考察数组当前部分 的中间 元素,
如果中间元素刚好是要找的,就结束搜索过程;
如果中间元素小于所查找的值,那么左侧的只会更小,不会有所查找的元素,只需到右侧查找;
如果中间元素大于所查找的值同理,只需到左侧查找。
(均以升序 数组为例)
int binary_search (int start, int end, int key) {int ret = -1 ; int mid;while (start <= end){1 ); if (arr[mid] < key)1 ;else if (arr[mid] > key)1 ;else { break ;return ret;
二分查找的局限性:
数据结构:数组
针对:有序数据
适合处理静态数据,只能用在插入、删除操作不频繁,一次排序多次查找的场景中
数据量太小不适合二分查找:如果要处理的数据量很小,顺序遍历就足够了
数据量太大也不适合二分查找:数组为了支持随机访问的特性,要求内存空间连续 ,对内存的要求比较苛刻
查找第一个值等于给定值的元素 int start = 0 , end = N-1 ;while (start <= end){int mid = start + ((end - start) >> 1 );if (arr[mid] > key)1 ;else if (arr[mid] < key) 1 ;else {if ((mid == 0 ) || (arr[mid - 1 ] != key)) break ;else 1 ;
查找第一个大于等于给定值的元素 int start = 0 , end = N-1 ;while (start <= end){int mid = start + ((end - start) >> 1 );if (arr[mid] < key)1 ;else {if ((mid == N-1 ) || (arr[mid - 1 ] < key))break ;else 1 ;
递归 写递归代码的关键在于写递推公式
递归定义的两要素:
递归边界条件 :所描述问题的最简单情况递归体 :使问题向边界条件转化的规则
e.g. 计算n!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <stdio.h> long long fact (int n) long long f;if (n == 1 ) f = 1 ;else f = n * fact (n-1 );return f;int main () {int n;do {scanf ("%d" ,&n);while (n<=0 );printf ("%d! = %ld\n" , n, fact(n));return 0 ;
辗转相减法 int gcd (int m,int n) {int g;if (m < n)else if (n == 0 )else return g;
数字顺序输出 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <stdio.h> void sequence (int n) {if (n/10 != 0 )10 );printf ("%d" , n%10 );int main (void ) {int num;printf ("请输入一个整数:" );scanf ("%d" ,&num);if (num < 0 ){putchar ('-' );return 0 ;
数字逆序输出 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <stdio.h> void reverse (int n) {printf ("%d" ,n%10 );if (n/10 != 0 )10 );int main (void ) {int num;printf ("请输入一个整数:" );scanf ("%d" ,&num);if (num < 0 ){putchar ('-' );return 0 ;
字符串顺序输出 #include <stdio.h> void sequence () {char ch;if ((ch=getchar()) != '\n' ){putchar (ch);int main (void ) {printf ("请输入一个字符串:\n" );putchar ('\n' );return 0 ;
字符串逆序输出 #include <stdio.h> void reverse () {char ch;if ((ch=getchar()) != '\n' ){putchar (ch);int main (void ) {printf ("请输入一个字符串:\n" );putchar ('\n' );return 0 ;
求斐波那契数列的第n项 1 1 2 3 5 8 13
O ( l o g n ) O(log\ n) O ( l o g n ) int fib4 (int n) {return fib_it(1 ,1 ,n);int fib_it (int a,int b,int n) {if (n == 1 ) return a;else return fib_it(b, a+b, n-1 );
二分查找的递归实现 int binsearch (int list [], int bottom, int top, int key) {int mid;if (bottom > top) return -1 ;else {2 ;if (key == list [mid]) return mid;else if (key < list [mid])return binsearch(list , bottom, mid-1 , key);else return binsearch(list , mid+1 , top, key);
数字转字符串输出 1234 -> 1-2-3-4
void change (long n) {if (n / 10 ){10 );putchar ('-' );putchar (n%10 + '0' );else putchar (n + '0' );
辗转相除法(欧几里得算法)求最大公约数 计算公式gcd(m, n) = gcd(n, m % n)
long long gcd (long long m, long long n) {if (n == 0 ) return m;return gcd(n, m%n);
我们采用Euclid(欧几里得)算法来求最大公因子,其算法是:
输入两个正整数m和n。
用m除以n,余数为r,如果r等于0,则n是最大公因子,算法结束,否则(3)。
把n赋给m,把r赋给n,转2.。
C5016
编写程序,求N个有理数的和。分子/分母的形式给出,你输出的和也必须是有理数的形式。 第一行给出一个正整数N(≤100)。 输出上述数字和的最简形式 —— 即将结果写成整数部分 分数部分,其中分数部分写成分子/分母,要求分子小于分母,且它们没有公因子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> std ;inline long long gcd_ (long long a, long long b) { return (a == 0 ) ? b : gcd_(b % a, a); }inline long long gcd (long long a, long long b) { return (a < b) ? (gcd_(a, b)) : (gcd_(b, a)); }inline long long lcm (long long a, long long b) { return a * b / gcd(a, b); }struct Rat {long long a, b;Rat (long long aa = 0 , long long bb = 1 ) { a = aa, b = bb; }inline Rat operator +(Rat A, Rat B){long long g = gcd(abs (ret.a), ret.b);return ret;inline Rat operator+=(Rat &A, Rat B) { return A = A + B; }int main () {int n;scanf ("%d" , &n);0 , 1 );for (int i = 0 ; i < n; i++){scanf ("%lld/%lld" , &x.a, &x.b);if (x.a != 0 )if (abs (ans.a) >= ans.b)printf ("%lld " , ans.a / ans.b);if (ans.a % ans.b)printf ("%lld/%lld" , ans.a % ans.b, ans.b);return 0 ;
高精度计算 由于C语言中对于整型数据来说都有其数据表示范围,当某个整数超出整型数据表示范围时,将无法用一个整型变量来存储它。
加法 我们可以用数字字符串的形式来表示它们,然后通过对数字字符串进行相加就可以实现任意长度的大整数求和。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 #include <stdio.h> #include <conio.h> #include <string.h> #define N 20 int tag = 0 ; void beep () {printf ("\07" );void GetNumberStr (char s[], int n) {int i = 0 ;char ch;while (1 ){if (ch == '\r' )break ;if (ch == '\b' ){if (i > 0 ){printf ("%c %c" , ch, ch);else beep();continue ;if (ch < '0' || ch > '9' ){continue ;if (i < n){ printf ("%c" , ch);else beep();'\0' ; char AddChar (char ch1, char ch2) {char ch;'0' + ch2-'0' ) + tag;if (ch >= 10 ){1 ;return (ch - 10 + '0' ); else {0 ;return (ch + '0' ); void LeftTrim (char str[]) {int i;for (i = 0 ; str[i] == ' ' ; i++)strcpy (str, str+i);void AddNumberStr (char a[], char b[], char c[], int n) {int i, j, k;memset (c, ' ' , N+2 );strlen (a) - 1 ;strlen (b) - 1 ;while (i >= 0 && j >= 0 ) while (i >= 0 ) '0' );while (j >= 0 ) '0' );if (tag == 1 )'1' ;1 ] = '\0' ; int main () {char a[N+1 ] = {'\0' }, b[N+1 ] = {'\0' }, c[N+2 ];printf ("a = " );while (strlen (a) == 0 )printf ("\nb = " );while (strlen (b) == 0 )printf ("\na + b = %s \n" , c);return 0 ;
todo: e.g. oj 数列求和-加强版
除法 todo: pat 1017
素数 判断是否素数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 #include <stdio.h> #include <math.h> int main () {int m, flag = 1 ;scanf ("%d" , &m);for (i = 2 ; i <= sqrt (m); i++){if (m % i == 0 ){0 ;break ;if (flag) printf ("%d 是素数\n" , m);else printf ("%d 不是素数\n" , m);return 0 ;
埃拉托斯特尼筛法求素数 取一个从2开始的整数序列,通过不断划掉 序列中的非素数 的整数逐步确定序列里的素数。
令n为2,它是素数
划掉序列中n的所有倍数(n*2, n*3, n*4…)
找到n之后下一个未划掉的元素,它是素数,令n等于它并回到步骤2继续
用数组元素的代表对应整数,prime[i]代表整数i。
e.g. 100以内的素数
法一 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <stdio.h> int main () {int i, j, prime[101 ];0 ] = 0 ;1 ] = 0 ;for (i = 2 ; i <= 100 ; i++){for (i = 2 ; i <= 100 ; i++){for (j = i + 1 ; j <= 100 ; j++){if (prime[i] && prime[j] && prime[j] % prime[i] == 0 ){0 ;for (i = 0 ; i <= 100 ; i++){if (prime[i]){printf ("%d " , prime[i]);return 0 ;
法二 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <stdio.h> #define N 100 int main () {int prime[N+1 ] = {0 }, i, j;for (i = 2 ;i <= N; i++)1 ;for (i = 2 ; i*i <= N; i++){if (prime[i] == 1 ){ for (j = i*2 ; j <= N; j += i)0 ;for (i = 2 ,j = 0 ;i <= N; i++){if (prime[i] != 0 )printf ("%4d%c" ,i,((++j)%5 ==0 ?'\n' :' ' ));return 0 ;
质因子分解
C5047
输入一个大于1的整数,编写程序将其分解成若干个质因子(素数因子)积的形式。 将输入的正整数分解成若干个质因子积的形式,质因子的出现顺序按从小到大排列。如:40=2*2*2*5;
应该是用到了短除法的思想:3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 #include <stdio.h> int main () {int n, i;scanf ("%d" , &n);printf ("%d=" , n);for (i = 2 ; n != 1 ; ){if (n % i == 0 ){printf ("%d" , i);if (n != 1 ){printf ("*" );else {return 0 ;
字典序 字典序(Lexicographical Order)是一种字符串排序方式,类似于字典中单词的排列顺序。逐个 比较,直到找到不同的字符为止。
e.g.1 实验四2-10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <stdio.h> #include <string.h> #define NUM_COUNTRIES 8 int main () {char countries[NUM_COUNTRIES][20 ] = {"CHINA" , "JAPAN" , "KOREA" , "INDIA" , "CANADA" , "AMERICA" , "ENGLAND" , "FRANCE" int i, j;char temp[20 ];for (i = 0 ; i < NUM_COUNTRIES-1 ; i++){for (j = 0 ; j < NUM_COUNTRIES-1 -i; j++){if (strcmp (countries[j], countries[j+1 ]) > 0 ){strcpy (temp, countries[j]);strcpy (countries[j], countries[j+1 ]);strcpy (countries[j+1 ], temp);for (i = 0 ; i < NUM_COUNTRIES; i++){printf ("%s\n" , countries[i]);return 0 ;
e.g.2 输入多个城市的名字,按升序排列输出。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <stdio.h> #include <string.h> #define CITYNUM 10 int main () { int i, j, k, num;char city[CITYNUM][20 ];char str[80 ];0 ; for (i = 0 ; i < CITYNUM; i++){printf ("input the name of the %dth city: " , i+1 );if (str[0 ] == 0 ) break ; if (strlen (str) > 19 ){continue ;strcpy (city[i], str); for (i = 0 ; i < num-1 ; i++){for (j = i+1 ; j < num; j++) if (stricmp(city[k], city[j]) > 0 ) if (k != i){strcpy (str, city[i]);strcpy (city[i], city[k]);strcpy (city[k], str);for (i = 0 ; i < num; i++)printf ("%s " , city[i]);printf ("\n" );
位运算 快速模2 temp & 1等价于temp % 2
C5033
编写程序,计算给定的一系列正整数中奇数的和。 在一行中给出一系列正整数,其间以空格分隔。 输出正整数序列中奇数的和。
int ans = 0 , temp;while (1 ){scanf ("%d" , &temp);if (temp <= 0 ) break ;1 ) * temp;printf ("%d\n" , ans);
无中间变量的值交换
位运算代替乘法 n << 1 等价于 n * 2
位运算代替除法 n >> 1 等价于 n / 2
对于 n 是有符号数的情况,当你可以保证 n ≥ 0 时,n >> 1 比 n / 2 指令数更少。
求出该数的各位数字 利用整除运算符/及求余运算符%按下述公式求得:
m / 1 0 p % 10 m/10^{p}%10 m /1 0 p %10
当p=0 时求得的是个 位数字,当p=1 时求得十 位数字,当p=2 时求得百 位数字。
利用这种方法可以使用循环结构得到位数不定 的任意整数的逆序。
还可以用于计算所有数字之和,判断回文数。
逆序输出正整数
计算数字的位数
使用公式提取每一位数字,并逐步将新提取的数字(digit)添加到 reversed 的末尾
通过 reversed * 10 将当前的 reversed 值向左移动一位,为新的数字腾出空间。
然后通过 + digit 将新提取的数字添加到 reversed 的末尾。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 int reverseNumber (int num) {int reversed = 0 ;int p = 0 ;int temp = num;while (temp != 0 ) {10 ;for (int i = 0 ; i < p; i++) {int digit = num / (int )pow (10 , i) % 10 ;10 + digit;return reversed;
求任意正整数中的最大数字 num % 10; -> 获取num的最后一位
num /= 10; -> 去掉num的最后一位
#include <stdio.h> int main () {int num, max = 0 ;scanf ("%d" , &num);while (num != 0 ){if (num % 10 > max){10 ;10 ;printf ("%d" , max);return 0 ;
拆数 读入一个整数num,统计该数的位数。
语言基础
基本输入输出
ctype.h 是 C 标准库中的一个头文件,提供了用于字符分类和转换的函数。这些函数主要用于检查字符是否属于某种类别(如字母、数字、空白符等),以及进行简单的字符转换(如大小写转换ch2=toupper(ch1);)。
conio.h 是一个非标准的 C 语言头文件,主要用于提供一些控制台输入输出功能。这个名字来源于 “Console Input/Output” 的缩写。提供了一些函数如:getch() 和 getche():获取单个字符输入,但 getch() 不回显到屏幕上,而 getche() 则会回显。
两次调用scanf()时,应使用getchar()吸收掉上次遗留的换行符和空格等。fflush(stdin)清空键盘缓存区是未定义行为。
数组
memset()是对内存的每个字节 单元都赋值为ch,所以主要适合字节型数组的整体赋值与对非字节型数组的清零。
puts() - 向显示器输出字符串并自动换行gets() - 输入以回车结束 的字符串
处理字符串中的每一个字符的模板
char str[10 ]="hello" ;for (i=0 ; str[i]!='\0' ; i++){
sprintf()用于将格式化的数据写入字符串中。\0)。失败时,返回一个负值。
#include <stdio.h> int main () {char buffer[50 ];int n = 123 ;sprintf (buffer, "The number is %d" , n);printf ("%s\n" , buffer); return 0 ;
指针
在引用指针变量所指向的内容之前,必须对指针进行赋值,即将指针指向已经定义的变量或常量。可用的 内存单元
结构与联合
利用typedef语句为结构类型起别名,格式为:typedef 类型名 类型名的别名;类型名的别名。
常见题型 数字相关的计算 求完数 实验三1-3,模拟考
n以内的斐波那契数 实验三1-10
#include <stdio.h> int main () {int f1 = 1 , f2 = 1 , n;scanf ("%d" , &n);printf ("%d %d " , f1, f2);while (f2 < n){int temp = f2;if (f2 < n)printf ("%d " , f2);return 0 ;
守形数
C5014
输出[m,n]范围内的守形数。
输入包含2个正整数m和n,之间用空格隔开。2≤m≤n≤10000
输出所有满足条件的整数,整数之间用1个空格隔开,行首行末均无空格。如果不存在,请输出”No exist”。
https://gitee.com/journey-of-dawn/wust-oj
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <stdio.h> int main () {int m, n, k, t, s, flag = 0 ;scanf ("%d %d" , &m, &n);for (int i = m; i <= n; i++){1 ; while (t){10 ; 10 ;if ((k % s) == i){if (flag == 1 )printf ("%d" , i);else printf (" %d" , i);if (flag == 0 )printf ("No exist" );return 0 ;
进制转换
21年期末程序填空题
int DeToBi (int db[], int n) {int i = 0 , r;do {2 ; 2 ; while (n); return i;
【例6.11】进制转换:将十六进制数字串转换成整数,假定字符串中不含任何非法字符
本例为模拟scanf函数的%x所实现的功能 输入的前缀0x或0X 进制的基数 对于数字字符、大写字母、小写字母应分别考虑
int i = 0 , number = 0 ;'0' && (str[i+1 ]=='x' || str[i+1 ]=='X' ) ? i+=2 : i;for ( ; str[i] != '\0' ; i++){ if (str[i]>='0' && str[i]<='9' ) 16 +str[i]-'0' ;else if (str[i]>='a' && str[i]<='f' ) 16 +str[i]-'a' +10 ; else if (str[i]>='A' && str[i]<='F' ) 16 +str[i]-'A' +10 ; printf ("%s=%d\n" ,str,number);
日期计算 计算该年中的第几天 实验五2-5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <stdio.h> int mday (int y, int m) {int m_list[] = {0 , 31 , 28 , 31 , 30 , 31 , 30 , 31 , 31 , 30 , 31 , 30 , 31 };if ((y % 4 == 0 && y % 100 != 0 ) || (y % 100 == 0 && y % 400 == 0 ))2 ]++;return m_list[m];int nday (int y, int m, int d) {int i, sum = 0 ;for (i = 1 ; i < m; i++){return sum;int main () {int ret, y, m, d;while (1 ){printf ("输入“年 月 日”:" );scanf ("%d%d%d" , &y, &m, &d);if (m >= 1 && m <= 12 && (d <= mday(y, m))) break ;else printf ("输入有误,重新输入\n" );printf ("%d" , ret);return 0 ;
字符串操作 求两字符串交集
22年期末程序填空题
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <stdio.h> #include <string.h> void find (char *s1, char *s2, char *s) {for ( ; *s1 != '\0' ; s1++){char *p = s2;for ( ; *p != '\0' ; p++)if (*s1 == *p) break ;if (*p != '\0' ){char *q = s;for ( ; *q != '\0' ; q++)if (*p == *q) break ;if (*q == '\0' )int main () {char s1[80 ], s2[80 ], s[80 ];memset (s, 0 , sizeof (s));scanf ("%s%s" , s1, s2);if (strlen (s) != 0 )puts (s);else printf ("No" );return 0 ;
删除相同字符
例:从字符串中删除与所给字符相同的字符并压缩字符串
如:字符串为char s[20]=”AABBBcBB”;
int i, j;char key = 'B' ;for (i=0 , j=0 ; s[i]!='\0' ; i++){if (s[i] != key) '\0' ;
判断回文字符串 int fun (char *s) {char *p1, *p2;while (*p2) p2++;while (p1 < p2)if (*p1++ != *p2--)return 0 ;return 1 ;
字符串匹配 todo: 数组3ppt p48